2.2 mediatriz y biseltriz

LA MEDIATRIZ Y BISELTRIZ SON
La bisectriz de un angulo es la recta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geometrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirectasde un ángulo.

Propiedades

Los puntos de la bisectriz son equidistantes a los dos lados del ángulo
Dos rectas, al cruzarse, determinan cuatro ángulos y sus bisectrices se cortan conformando ángulos rectos ente ellas.

En la figura, la bisectriz del ángulo xOy (en amarillo) es (zz'), y la del ángulo x'Oy es (ww'). Se cortan formando un ángulo recto. En efecto, si llamamos a la amplitud de xOz, y b la de yOw, observamos que 2a + 2b es la amplitud del ángulo xOx' = 180º, es un ángulo plano. Luego zOw mide a + b = 90º.

Aplicación en triángulos

Las tres bisectrices de los ángulos internos de un triángulo se cortan en un único punto, que equidista de los lados. Este punto se llama el incentro  del triángulo y es el centro de la circunferencia inscrita al triángulo. Esta circunferencia es tangente a cada uno de los lados del triángulo.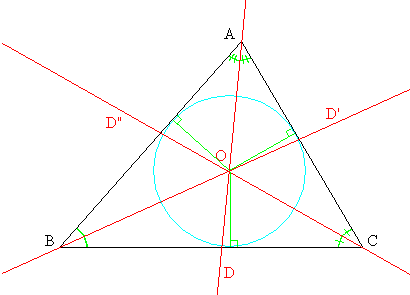

Demostración: Dos bisectrices del triángulo no pueden ser paralelas. Sea O la intersección de las bisectrices D y D' (ver figura). Como O pertenece a D, es equidistante de las rectas (A,B) y (A,C). Como O pertenece a D', entonces también equidista de las rectas (AB) y (BC). Por transitividad de la igualdad, es equidistante de (A,C) y (B,C), y pertenece a la bisectriz (interior) del ángulo C, es decir a D". Al ser equidistante a los tres lados. Se sigue que la circunferencia cuyo radio sea justamente la distancia común del punto O a los lados del triángulo es tangente a cada uno de los lados.

LA MEDIATRIZ:
La mediatriz de un segmentoes larecta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como la recta cuyos puntos son equidistantes a los extremos del segmento. También se la llama simetral. Lugar geometrico de los puntos que equidistan de los extremos de un segmento AB.

Construcción gráfica de la mediatriz con reglas y compas

 

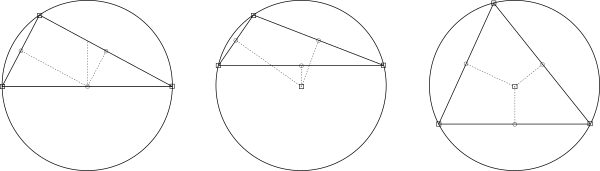
Las mediatrices de un triángulo se denomina circuncentro, el cual es el centro de la circunferencia que pasa por los vértices del triángulo, es decir, de la circunferencia circunscrita al triángulo.

ejmplo

En efecto, sea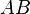 un segmento delimitado por los puntos y 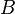(véase la figura 1). Sea el punto medio del segmento y la recta perpendicular al segmento por dicho punto. Sea un punto sobre la recta . En la isimetria axial respecto de la recta , el punto es invariante y los puntos y 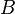son uno el simétrico del otro. Por tanto, en esta simetría, el segmento se transforma en el segmento , ambos segmentos son congruentes y el punto equidista de los puntos y 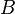. En consecuencia, todo punto que se encuentre sobre la recta pertenece a la mediatriz del segmento en cuestión.

 

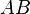Recíprocamente, (véase figura 2) sea un segmento y sea un punto que equidista de y de 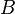, esto es, que los segmentos y son iguales. Consideremos la bisectriz del ángulo y sea la intersección de dicha bisectriz con el segmento .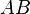
Por construcción, los ángulos y son iguales y en la simetría axial respecto de la recta se transforman uno en el otro. Como los segmentos y son iguales en esta simetría, los puntos y 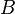son uno la imagen del otro. Concluimos que el punto es punto medio del segmento 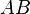y que dicho segmento es perpendicular a la recta .

 

En todotriangulo ABC las mediatrices de sus tres lados concurren en un mismo punto, llamado el circuentro(O) del triángulo. Dicho punto equidista de los vértices del triángulo. Lacircunferencia de centro O y de radio OA, pasa por los otros dos vértices del triángulo. Se dice que dicha circunferencia es circunscrita al triángulo y que el triángulo está inscrito en la circunferencia.

La mediatriz de una cuerda pasa por el centro de la circunferencia.